5 - 固定池大小的汇总流行率和具有已知灵敏度和特异性的测试
These methods use frequentist approaches to estimate prevalence and confidence limits, assuming a fixed pool size and a test with known values for sensitivity and specificity, as described below.
方法3
这种方法(方法4来自Cowling等人。(1999年) assumes a fixed pool size and that test sensitivity and specificity are known exactly (no uncertainty about their values). Confidence limits are based on a normal approximation and may be <0 for low prevalence values.
流行率估计为: 
和标准误差(SE(p)): 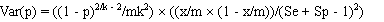
哪里:
- p =患病率;
- k =池大小;
- m =测试的池数;
- x =正池的数量;
- Se =测试的灵敏度;和
- Sp =测试的特异性;
使用正态近似计算渐近置信限:
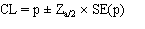
哪里  是对应于所需置信限的标准化正态变量.
是对应于所需置信限的标准化正态变量.
此方法所需的输入是:
- 游泳池大小;
- 测试的池数;
- 池数正面;
- 假定测试的敏感性;
- 假设测试的特异性;和
- 期望的上限和下限置信度.
Pool size, number of pools and number of pools positive must be positive integers and the number of positive pools must be less than the number of pools tested. Sensitivity and specificity must be >0 and <=1 and upper and lower confidence limits must be >0 and <1.
产出包括:
- 估计动物水平的流行率;
- 上下渐近置信限;
- 估计的标准误差;和
- 所有可能结果的估计和置信度的图形和文本文件(通过单击相应的图标下载).
Estimates are only valid if the proportion of positive pools is greater than the false positive rate (1 - Specificity) and less than or equal to the true positive rate (Sensitivity). Invalid results are indicated by NA in the results table.
方法4
这种方法(方法5来自Cowling等人。(1999年)) 假设一个固定的池大小,并且确切地知道测试的灵敏度和特异性(没有关于它们的值的不确定性)。 确切的置信限度基于二项式理论,因此置信限度永远不会<0或> 1.
流行率和方差估计如下方法3: 
和: 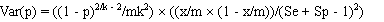
哪里:
- p =患病率;
- k =池大小;
- m =测试的池数;
- x =正池的数量;
- Se =测试的灵敏度;和
- Sp =测试的特异性.
Exact confidence limits are estimated by calculating the corresponding binomial confidence limits for the proportion of positive pools and then transforming these back to individual-level prevalence values using the equation for estimating prevalence from 方法3.
此方法所需的输入是:
- 游泳池大小;
- 测试的池数;
- 池数正面;
- 假定测试的敏感性.
- 假设测试的特异性;和
- 期望的上限和下限置信度.
Pool size, number of pools and number of pools positive must be positive integers and the number of positive pools must be less than the number of pools tested. Sensitivity and specificity must be >0 and <=1 and upper and lower confidence limits must be >0 and <1.
产出包括:
- 估计动物水平的流行率;
- 上下精确(二项式)置信限;
- 估计的标准误差;和
- 所有可能结果的估计和置信度的图形和文本文件(通过单击相应的图标下载).
Estimates are only valid if the proportion of positive pools is greater than the false positive rate (1 - Specificity) and less than or equal to the true positive rate (Sensitivity). Invalid results are indicated by NA in the results table.
« 前 下 »
| 内容 | |
|---|---|
| 1 | 介绍 |
| 2 | 概观 |
| 3 | 贝叶斯与Frequentist方法 |
| 4 | 固定泳池大小和完美测试 |
| 5 | 固定的游泳池大小和已知的Se&Sp |
| 6 | 固定的游泳池大小和不确定的Se&Sp |
| 7 | 可变池大小和完美测试 |
| 8 | 使用Gibbs采样器汇集流行率 |
| 9 | 使用一次测试确实流行 |
| 10 | 使用Gibbs采样器进行两次测试估计真实患病率 |
| 11 | 估计先前Beta分布的参数 |
| 12 | 样本大小,完美的游泳池大小和完美的测试 |
| 13 | 固定池的样本大小和已知的测试灵敏度和特异性 |
| 14 | 固定池大小的样本大小和不确定的测试灵敏度和特异性 |
| 15 | 模拟固定池大小的采样 |
| 16 | 模拟可变池大小的采样 |
| 17 | 重要假设 |
| 18 | 汇总流行率估计有偏见! |





